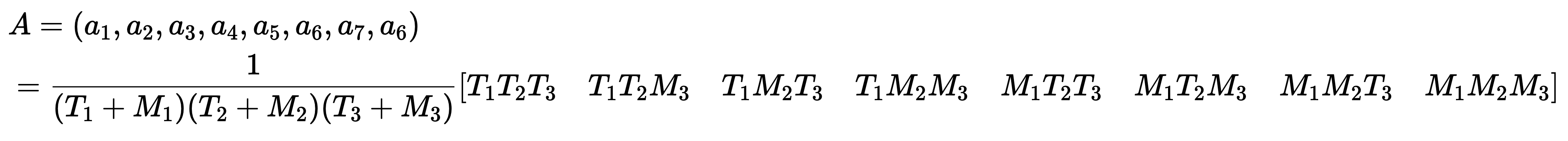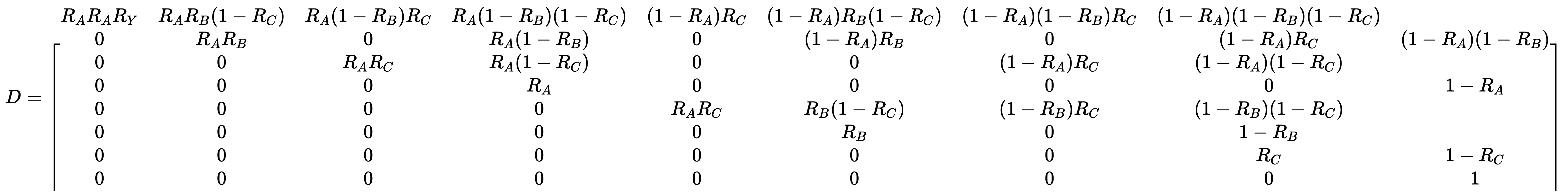本文针对ADC模型,抛开推导过程,从算法实现角度进行阐述。
正文含少量MathJax公式,加载异常刷新即可。
前言
系统的效能是指某系统在规定的条件下达到规定使用目标的能力,是目标系统完成规定任务程度的度量,能从总体上描绘出一个对象在特定环境下完成规定任务的实际能力。
为更加清晰阐述算法实现,将以导弹武器系统为例进行描述。
可用性分析
表示可用性向量,表征系统在执行任务之前的状态。
假设系统有 $n$ 种不同的状态,且在任一时刻系统处于状态 $i$ 的概率为 $a_i$,则可用性向量 $A=(a_1, a_2, \cdots, a_n)$ 表示。
设 A、B、C 分别表示发射平台、飞航导弹和技术保障设备 3 个系统,这 3 个系统的平均故障间隔时间分别表示为 $T_1$、$T_2$、$T_3$,平均故障修复时间分别为 $M_1$、$M_2$、$M_3$。3 个组成部分在工作时有 8 种工作状态,从 $(ABC)$ 示三部分全部处于正常状态、$(AB\overline{C})$ 示发射平台和飞航导弹正常、技术保障设备故障,到 $(\overline{A}\overline{B}\overline{C})$ 表示三部分全部处于故障状态等八个。
可用度是该系统处于工作状态的概率,计算公式如下:
$$ \begin{cases} A_A=\frac{T_1}{T_1+M_1}\\ A_B=\frac{T_2}{T_2+M_2}\\ A_C=\frac{T_3}{T_3+M_3} \end{cases} $$
推算步骤省略,可计算得到系统可用性向量:
可信性分析
可信性是指系统在任务开始时可用性给定的情况下,规定的任务剖面中的任一随机时刻,能够使用且能完成规定任务的能力。
可信性在概念上与可靠性有相似之处。可信性参数矩阵:
$$D(t)=\begin{bmatrix}d_{11}&d_{12}&\cdots&d_{1n}\\d_{21}&d_{22}&\cdots&d_{2n}\\\cdots&\cdots&\cdots&\cdots\\d_{n1}&d_{n2}&\cdots&d_{nn}\end{bmatrix}$$
式中:$d_{ij}$表示若系统在开始执行任务时处于状态$i$,系统在执行任务过程中处于状态$j$的概率;$t$表示执行任务的时间。
系统运行过程中的可靠性函数为指数函数,并由下式给出:
因此,发射平台、飞航导弹和技术保障设备的可靠性如下:
$$ R_A=\exp\left(-\frac{t}{T_1}\right) $$
$$ R_B=\exp\left(-\frac{t}{T_2}\right) $$
$$ R_C=\exp\left(-\frac{t}{T_3}\right) $$
基本的转移概率为:
$$ \begin{aligned} &P(A\to A)=R_{A},\quad P(B\to B)=R_{B}, \\ &P(C\to C)=R_{C},\quad P(A\to\overline{A})=1-R_{A}, \\ &P(B\to\overline{B})=1-R_{B},\quad P(C\to\overline{C})=1-R_{C}, \\ &P(\overline{A}\to A)=0,\quad P(\overline{B}\to B)=0,\quad P(\overline{C}\to C)=0, \\ &P(\overline{A}\to\overline{A})=1,\quad P(\overline{B}\to\overline{B})=1,\quad P(\overline{C}\to\overline{C})=1 \end{aligned} $$
定义$d_{ij}=P\left\{t\text{ 时间内状态}i\text{ 转移到状态 }j\right\}$
可得到系统的可信性参数矩阵:
能⼒分析
能⼒矩阵$C$是描述系统处于$n$个状态时,完成规定任务的固有能⼒。$C$是⼀个具有$n$个元素的列向量。
$$C=(c_1,c_2\cdots c_j\cdots c_n)^\mathrm{T}$$
$p_1$表⽰发射平台状态良好,能顺利完成发射任务的概率;$p_2$表⽰导弹发射后,飞⾏过程中各部件⼯作状态良好,能够完成制导、突防以及有效打击对⽅⽬标的概率;$p_3$表⽰技术保障设备状态良好,能够成功保障顺利发射的概率。
$p_1^{\prime}$表示发射平台发⽣故障,但能顺利完成发射任务的概率;$p_2^{\prime}$表示导弹发射后,⻜⾏过程中某部件发⽣故障,但能够完成制导、突防以及有效打击对⽅⽬标的概率;$p_3^{\prime}$表示技术保障设备发⽣故障,能够保障顺利发射的概率。
故能力参数如下:
$$ \begin{aligned} &c_1=p_1p_2p_3, \\ &c_2=p_1p_2p_3^{\prime}, \\ &c_3=p_1p_2^{\prime}p_3, \\ &c_4=p_1p_2^{\prime}p_3^{\prime}, \\ &c_5=p_1^{\prime}p_2p_3, \\ &c_{6}=p_1^{\prime}p_2p_3^{\prime}, \\ &c_{7}=p_1^{\prime}p_2^{\prime}p_3, \\ &c_{8}=p_1^{\prime}p_2^{\prime}p_3^{\prime} \end{aligned} $$
能⼒参数矩阵应表⽰为:
$$ C=\begin{bmatrix}c_1\\c_2\\c_3\\c_4\\c_5\\c_6\\c_7\\c_8\end{bmatrix}=\begin{bmatrix}p_1p_2p_3\\p_1p_2p_3^{\prime}\\p_1p_2^{\prime}p_3\\p_1p_2^{\prime}p_3^{\prime}\\p_1^{\prime}p_2p_3\\p_1^{\prime}p_2p_3^{\prime}\\p_1^{\prime}p_2^{\prime}p_3\\p_1^{\prime}p_2^{\prime}p_3^{\prime}\end{bmatrix} $$
效能模型
令 $F=D\cdot C$、$F_i = \sum_{j=1}^{8} D_{ij} \cdot C_j$
$$ E = A\cdot D\cdot C= \sum_{k=1}^{8} A_k \cdot F_k $$
实现Demo
#include <iostream>
#include <vector>
#include <cmath>
class SystemAvailability {
public:
// Constructors to initialize the time and maintenance arrays
SystemAvailability(double t1, double m1, double t2, double m2, double t3, double m3)
: T1(t1), M1(m1), T2(t2), M2(m2), T3(t3), M3(m3) {}
// Method to compute the availability vector
std::vector<double> computeAvailability() {
double A1 = T1 / (T1 + M1);
double A2 = T2 / (T2 + M2);
double A3 = T3 / (T3 + M3);
return {
A1 * A2 * A3,
A1 * A2 * (1 - A3),
A1 * (1 - A2) * A3,
A1 * (1 - A2) * (1 - A3),
(1 - A1) * A2 * A3,
(1 - A1) * A2 * (1 - A3),
(1 - A1) * (1 - A2) * A3,
(1 - A1) * (1 - A2) * (1 - A3)
};
}
private:
double T1, M1, T2, M2, T3, M3;
};
class SystemReliability {
public:
SystemReliability(double t, double t1, double t2, double t3)
: time(t), T1(t1), T2(t2), T3(t3) {}
std::vector<std::vector<double>> computeReliabilityMatrix() {
double RA = std::exp(-time / T1);
double RB = std::exp(-time / T2);
double RC = std::exp(-time / T3);
return {
{RA*RB*RC, RA*RB*(1-RC), RA*(1-RB)*RC, RA*(1-RB)*(1-RC), (1-RA)*RB*RC, (1-RA)*RB*(1-RC), (1-RA)*(1-RB)*RC, (1-RA)*(1-RB)*(1-RC)},
{0, RA*RB, 0, RA*(1-RB), 0, (1-RA)*RB, 0, (1-RA)*(1-RB)},
{0, 0, RA*RC, RA*(1-RC), 0, 0, (1-RA)*RC, (1-RA)*(1-RC)},
{0, 0, 0, RA, 0, 0, 0, 1-RA},
{0, 0, 0, 0, RB*RC, RB*(1-RC), (1-RB)*RC, (1-RB)*(1-RC)},
{0, 0, 0, 0, 0, RB, 0, 1-RB},
{0, 0, 0, 0, 0, 0, RC, 1-RC},
{0, 0, 0, 0, 0, 0, 0, 1}
};
}
private:
double time, T1, T2, T3;
};
class SystemCapability {
public:
SystemCapability(double p1, double p2, double p3, double p1_prime, double p2_prime, double p3_prime)
: P1(p1), P2(p2), P3(p3), P1_prime(p1_prime), P2_prime(p2_prime), P3_prime(p3_prime) {}
// Method to compute the capability vector
std::vector<double> computeCapability() {
return {
P1 * P2 * P3,
P1 * P2 * P3_prime,
P1 * P2_prime * P3,
P1 * P2_prime * P3_prime,
P1_prime * P2 * P3,
P1_prime * P2 * P3_prime,
P1_prime * P2_prime * P3,
P1_prime * P2_prime * P3_prime
};
}
private:
double P1, P2, P3, P1_prime, P2_prime, P3_prime;
};
int main() {
// Availability calculations
SystemAvailability availability(100, 20, 150, 25, 200, 30);
std::vector<double> availabilityVector = availability.computeAvailability();
// Reliability calculations
SystemReliability reliability(50, 100, 150, 200);
auto reliabilityMatrix = reliability.computeReliabilityMatrix();
// Capability calculations
SystemCapability capability(0.9, 0.85, 0.95, 0.8, 0.8, 0.9);
std::vector<double> capabilityVector = capability.computeCapability();
// Placeholder for performance calculation based on A, D, C
double performanceMetric = 0;
for (size_t i = 0; i < 8; ++i) {
double Fi = 0;
for (size_t j = 0; j < 8; ++j) {
Fi += reliabilityMatrix[i][j] * capabilityVector[j];
}
performanceMetric += availabilityVector[i] * Fi;
}
std::cout << "Performance Metric: " << performanceMetric << std::endl;
return 0;
}
SystemAvailability、SystemReliability 和 SystemCapability,用于分别计算可用性、可信性和能力矩阵。
之前看过一个知乎帖子,说是代码里std::出现次数和代码水平成反比,我觉得他说的对,因为我能写就写,且代码能力低下。